Premiers modèles prédictifs

Objectif : passer de la description à la prédiction sur nos données locales, en restant simple et lisible. On compare quelques approches de base sur les horizons T+10, T+60, T+360 (~6 h) et T+1440 (~24 h) pour température, vent et pluie, sans présupposer que ça va marcher à tous les coups.

python "docs/09 - Premiers modèles prédictifs/scripts/run_baselines.py"

Le script génère :

deux CSV de résultats dans docs/09 - Premiers modèles prédictifs/data/ :
- baselines_regression.csv (température/vent, MAE/RMSE, splits validation/test)
- baselines_rain.csv (pluie binaire, précision/rappel/F1/Brier, splits validation/test)
deux figures de synthèse (validation) dans docs/09 - Premiers modèles prédictifs/figures/ :
- baselines_mae_validation.png (MAE vs horizon pour température et vent)
- baselines_rain_validation.png (F1 et Brier vs horizon pour la pluie)

python "docs/09 - Premiers modèles prédictifs/scripts/run_first_models.py"

Ce second script :

construit les variables dérivées (sin/cos temporels, lags, deltas, moyennes glissantes, vent u/v, drapeaux) à partir du CSV brut ;
découpe en train/validation/test (70/15/15 %) ;
utilise la matrice de corrélation décalée (chapitre 5) pour privilégier les variables/lags dont |r| ≥ 0,2, tout en conservant les cibles ; l’humidité, la pression, l’illuminance, etc. sont donc injectées quand elles sont corrélées à la cible ;
entraîne Ridge/Lasso pour température et vent, régression logistique pour la pluie ;
exporte models_regression.csv et models_rain.csv dans docs/09 - Premiers modèles prédictifs/data/ ;
produit models_mae_validation.png (MAE vs horizon pour température et vent) dans docs/09 - Premiers modèles prédictifs/figures/.

Données et préparation

Jeu principal : data/weather_minutely.csv (pas 10 min), mis à jour au fil du temps. On peut réutiliser les CSV dérivés (matrices de lags/corrélations du chapitre 5) pour choisir des lags pertinents et vérifier la cohérence.
Variables dérivées reprises du chapitre 8 : temps en sin/cos, lags courts (T-10/-20/-30), deltas (variation récente), moyennes/cumul sur 30–60 min, composantes (u, v) du vent, drapeaux d’événements (pluie en cours, vent fort, chaleur/froid).
Normalisation : on calcule moyenne/écart-type sur la partie train uniquement, puis on applique ces paramètres aux parties validation et test pour ne pas utiliser d’informations futures.

Découpage et validation

Découpe sans fuite : train (début→~70 %), validation (~15 % suivant), test (~15 % le plus récent), tout en ordre chronologique.
Variante robuste : time-series split “en rouleau”, où l’on répète plusieurs découpes successives ; chaque paire (train, validation) est un fold. Cela aide à voir si un modèle reste stable dans le temps.

Références de comparaison (baselines)

Persistance : prédire que la prochaine valeur est identique à la dernière observée (par horizon).
Climatologie horaire : moyenne ou quantiles par heure locale (et éventuellement par saison) pour température/vent ; fréquence de pluie par heure pour la pluie.
Moyenne mobile : prolonger la moyenne des 30–60 dernières minutes.
Pluie rare : classifieur “toujours sec” comme seuil minimal ; si un modèle ne fait pas mieux, il ne sert à rien.

Modèles simples à essayer

Régressions linéaires avec régularisation (Ridge/Lasso) pour température et vent : même principe que la régression linéaire, avec un terme qui limite l’ampleur des coefficients (Ridge) ou peut en annuler certains (Lasso) pour éviter le sur-apprentissage.
Régression logistique pour la pluie : fournit une probabilité de pluie plutôt qu’un oui/non, ce qui permet d’ajuster le seuil selon l’usage (prudence ou non).
Si besoin de non-linéarités : petits arbres de décision, random forest ou boosting légers pour capturer des relations plus courbes tout en restant interprétables.

Lecture des résultats

Température / vent : MAE et RMSE (définis au chapitre 8) pour juger l’erreur moyenne et la sensibilité aux grosses erreurs.
Pluie : précision, rappel, F1, Brier score et calibration des probabilités pour voir si les annonces de pluie sont réalistes et bien calibrées.
Multi-horizons : tracer l’erreur en fonction de l’horizon pour identifier à partir de quand la prévision décroche. On s’attend à ce que +24 h soit difficile sans contexte synoptique, et on documentera ces limites.

Déroulé proposé

Construire les variables dérivées et sauvegarder un jeu prêt pour l’apprentissage (en suivant le découpage temporel).
Évaluer les références (baselines) sur chaque horizon.
Entraîner les modèles simples (linéaires régularisés, logistique, éventuellement arbres légers) et comparer aux références.
Consolider l’évaluation multi-horizons (time-series split), conserver les résultats pour les chapitres suivants (affinements et pipeline d’inférence local).

Synthèse visuelle des baselines (validation)

Ce que montrent ces baselines

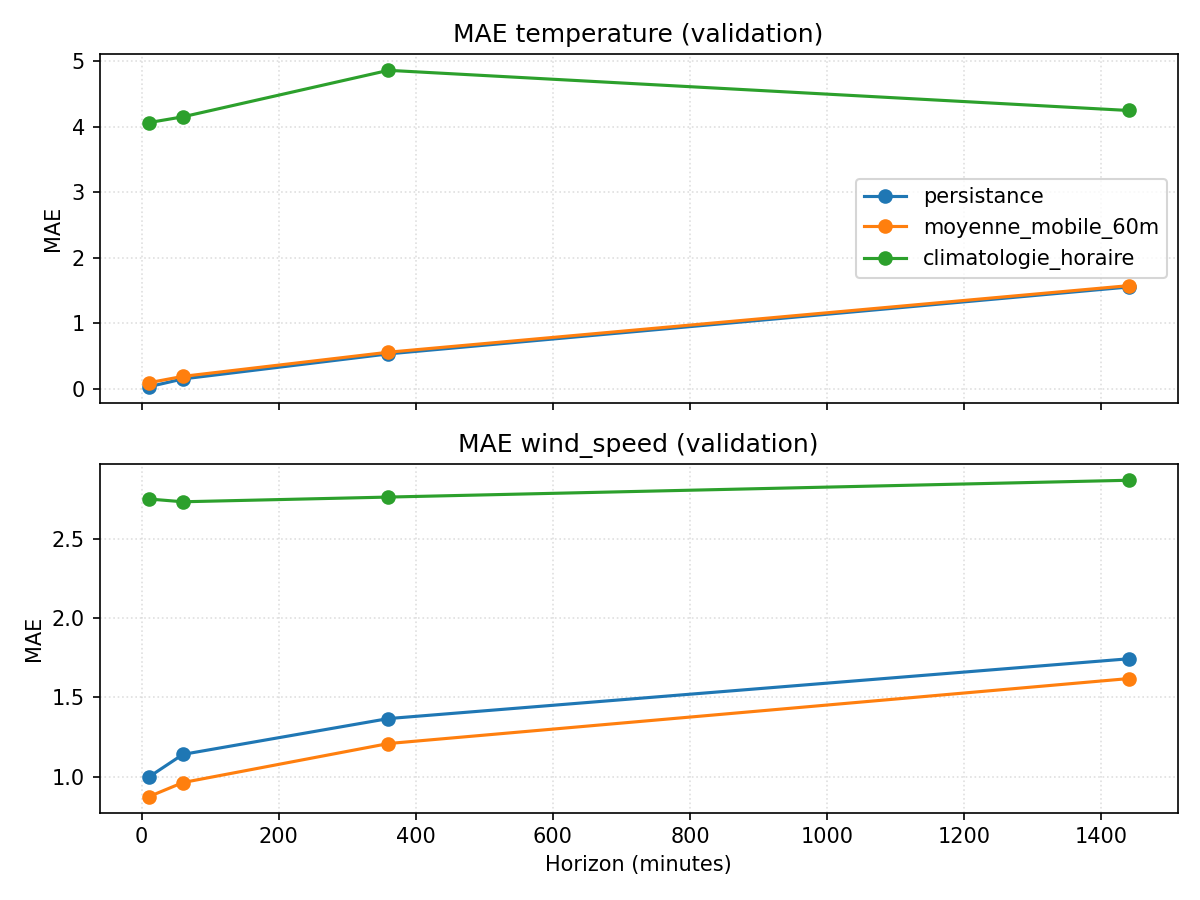
Température : la persistance reste imbattable jusqu’à +6 h avec une MAE < 1 °C ; au-delà (+24 h), l’erreur grimpe (≈1,5 °C) mais reste meilleure que la climatologie horaire qui plafonne autour de 4–6 °C. On part donc avec un avantage net sur le très court terme, mais l’horizon journalier sera plus difficile.
Vent : la moyenne mobile 60 min devance légèrement la persistance dès +10 min, mais l’écart reste faible et l’erreur croît avec l’horizon (MAE ≈2 km/h à +24 h). Le gain potentiel d’un modèle plus riche sera modeste si l’on reste sur ce pas de 10 min.
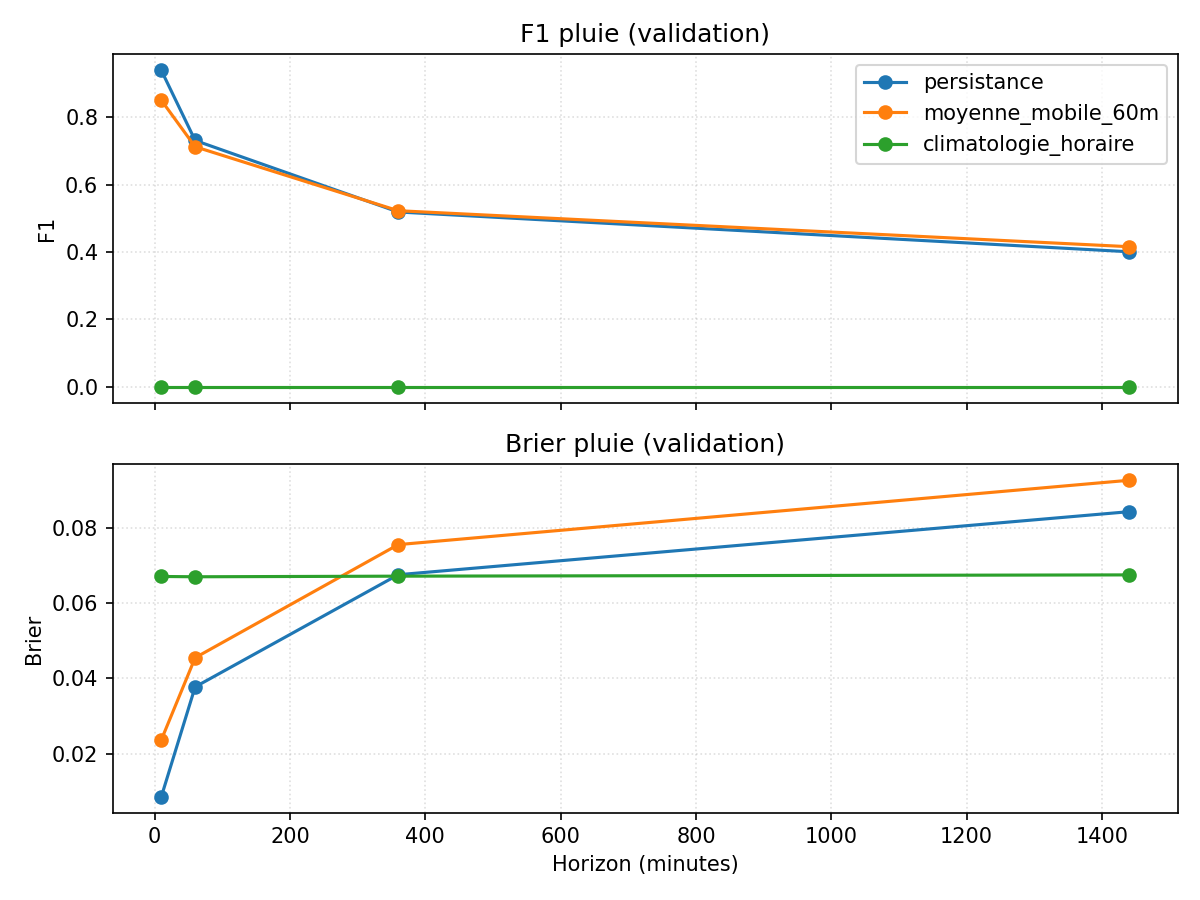
Pluie (binaire) : la persistance affiche des F1 élevés aux petits horizons parce que la pluie est rare et que “rester sec” gagne souvent ; le Brier augmente avec l’horizon, signe que la confiance se dégrade. La climatologie horaire est nulle : sans contexte, elle ne voit pas la pluie. Toute tentative de modèle devra donc battre la persistance sur F1/Brier, surtout à +60/+360 min où le score chute déjà.
Conclusion provisoire : les baselines définissent une barre à franchir — forte sur le très court terme (température/vent), beaucoup plus basse pour la pluie (où la rareté favorise la persistance). Les modèles devront prouver un gain net sur ces repères, en particulier sur les horizons intermédiaires (+60/+360 min) où la prévisibilité commence à décrocher.

Premiers modèles (Ridge/Lasso/logistique)

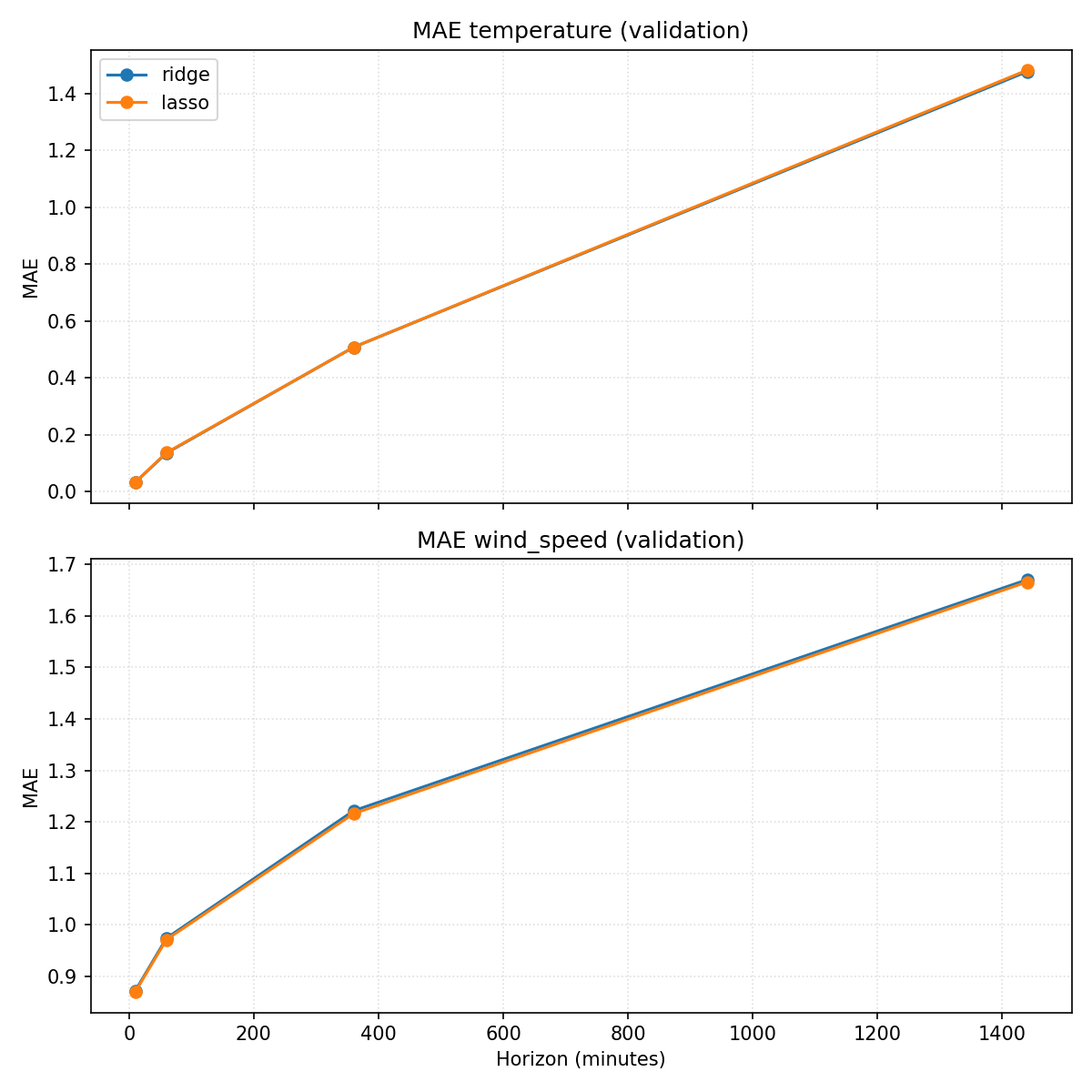
Température : Ridge/Lasso battent légèrement la persistance sur tous les horizons sauf à +10 min (MAE ≈0,14 à +60 min vs 0,15 pour la persistance ; ≈1,48 à +1440 vs 1,55). Injecter les variables corrélées (humiditié, illumination, pression…) donne un petit gain par rapport à la version “lags génériques”, mais la marge reste modeste.
Vent : même logique, un léger mieux que la persistance (≈0,87 à +10 min vs 0,99 ; ≈1,67 à +1440 vs 1,74). Les corrélations étant faibles, l’apport des autres variables reste limité.
Pluie : la régression logistique reste derrière la persistance (F1 ≈0,91 à +10 min contre 0,94 pour la persistance ; chute rapide à +60 et au-delà). La probabilité est calibrée (Brier ≈0,011 à +10 min), mais ne compense pas l’avantage de “rester sec”. Il faudra enrichir les features ou changer de modèle pour espérer dépasser la baseline.

En résumé, les modèles linéaires apportent un petit gain sur température/vent et échouent encore à battre la persistance pour la pluie. C’est une base de référence ; les prochains essais devront justifier leur complexité par un gain clair, surtout sur les horizons où les baselines se dégradent (+60/+360 min).

Conclusion provisoire du chapitre

Contre l’intuition, c’est au très court terme que nos modèles simples se heurtent à un mur pour la pluie : la persistance reste devant à +10 min, et l’écart se creuse déjà à +60 min. Pour la température et le vent, les gains existent mais restent modestes, même à +10 min, alors qu’on pouvait espérer les “faciles”. Les horizons longs se dégradent comme prévu, mais le vrai défi est donc d’améliorer les prédictions proches sans sur-complexifier. Prochaine étape : tester des modèles plus flexibles (arbres/boosting) et enrichir les features, tout en vérifiant que le gain sur les petits horizons justifie l’effort.

8.7 KiB Raw Blame History Unescape Escape