donnees_meteo/docs/10 - Modèles non linéaires/index.md

Modèles non linéaires (arbres, forêts, gradient boosting)

Objectif : tester des modèles plus flexibles que les régressions linéaires/logistiques, en restant raisonnables côté ressources. On utilise des forêts aléatoires (random forest) et du gradient boosting sur les mêmes horizons (T+10, T+60, T+360, T+1440) pour température, vent et pluie.

python "docs/10 - Modèles non linéaires/scripts/run_tree_models.py"

Le script :

• lit data/weather_minutely.csv et construit les variables dérivées (sin/cos, lags/deltas/moyennes, vent u/v, drapeaux) ;
• s’appuie sur la matrice de corrélation décalée (chapitre 5) pour prioriser les variables/lags avec |r| ≥ 0,2, tout en conservant les cibles ;
• sous-échantillonne l’apprentissage (1 ligne sur 10) pour contenir le temps de calcul, à garder en tête pour interpréter les scores ;
• découpe en train/validation/test (70/15/15 %) ;
• entraîne forêts et gradient boosting pour température/vent (régression) et pluie binaire (classification) ;
• exporte models_tree_regression.csv et models_tree_rain.csv dans docs/10 - Modèles non linéaires/data/ ;
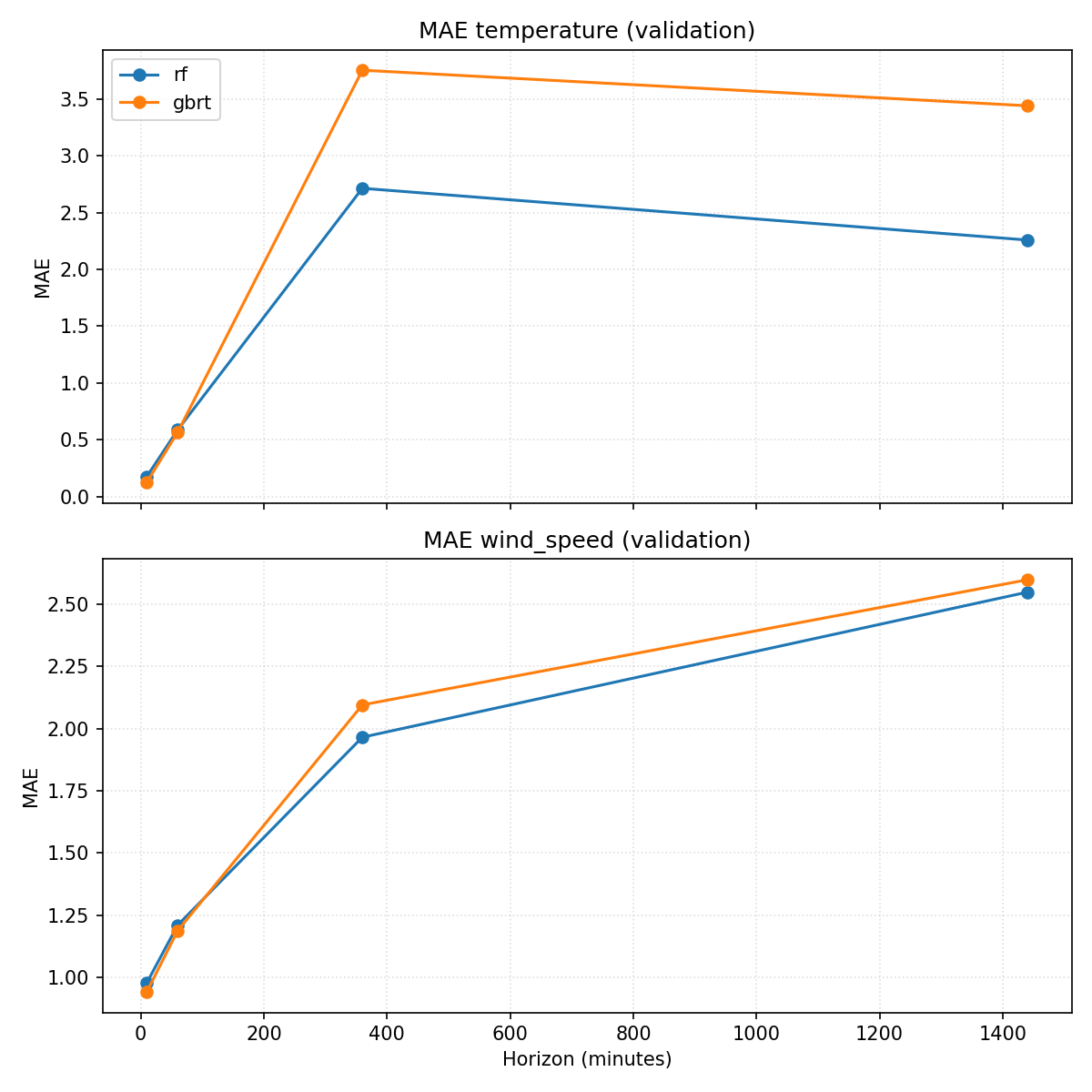
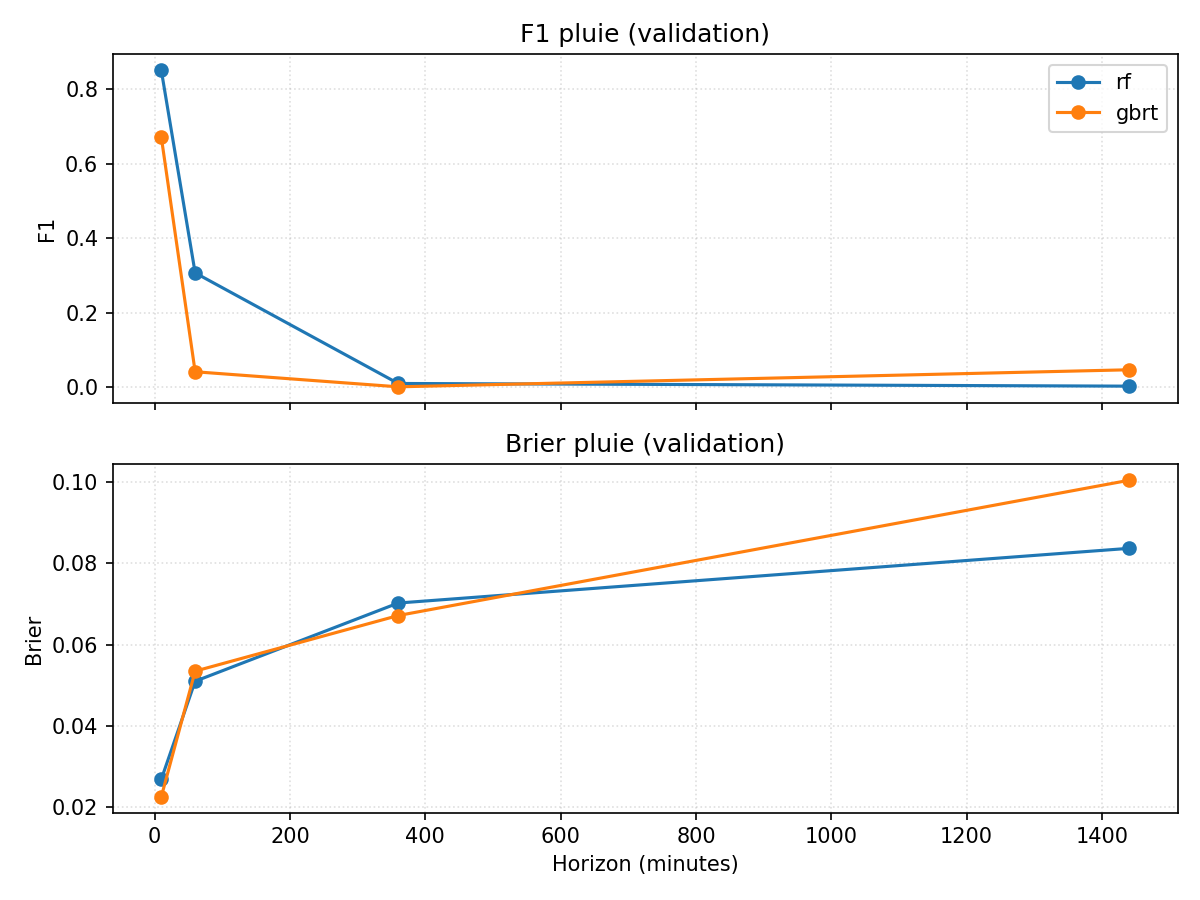
• génère deux figures (validation) dans docs/10 - Modèles non linéaires/figures/ :
  • models_tree_mae_validation.png (MAE vs horizon pour température et vent)
  • models_tree_rain_validation.png (F1 et Brier vs horizon pour la pluie)

Lecture rapide des résultats (validation)

• Température : le gradient boosting est meilleur que la forêt sur le très court terme (MAE ≈0,13 à +10 min), mais reste derrière les modèles linéaires du chapitre 9 (MAE ≈0,14 à +60 min avec Ridge). La sous‑utilisation des données d’apprentissage (1/10) pèse sur la performance.
• Vent : gains modestes, MAE ~0,94 à +10 min (GB) et ~1,19 à +60 min, sans dépassement clair des modèles linéaires précédents.
• Pluie : F1 ≈0,85 (forêt) et 0,67 (GB) à +10 min, mais toujours en dessous de la persistance (~0,94) ; le Brier reste modéré (~0,02–0,03). Aux horizons +60/+360/+1440, les scores retombent rapidement.

Conclusion provisoire

Ces modèles non linéaires apportent de la flexibilité mais, avec un apprentissage allégé pour tenir le temps de calcul, ils ne battent pas les baselines ni les modèles linéaires sur les horizons courts. Pour progresser, il faudra soit élargir l’échantillon d’apprentissage (temps de calcul plus long), soit régler finement les hyperparamètres, soit enrichir les features (ou combiner les deux), tout en vérifiant que le gain justifie l’effort.